Fractals discover the true beauty, which stays behind matemathical
formulas and computer algorithms. Although the are very similar to
objects from the real world, they are 100% digitally generated and
every single pixel here is a result of a computer calculation.

But it is more than an artistic affectation; it's a door to the fractal
universe, a good starting point to discover what lies beyond your
imagination. It's a fun, but it's also a challenge, so take a deep
breath and dive in ...

Fractal Experience includes 1042 pictures, located in 18 galleries.

https://www.fractalexperience.com/index.php

https://www.nahee.com/O/newton_b.html

frac·tal (frâk´tël) n.   A geometric
pattern that is repeated at ever smaller scales to produce irregular
shapes and surfaces that cannot be represented by classical geometry.  
Fractals are used especially in computer modeling of irregular patterns
and structures in nature.   [French, from Latin fractus, past participle of frangere, to break.   See FRACTION.]

Fractals are extensions of traditional Euclidean shapes, such as lines,
squares, and circles, with two fundamental properties.   First, when
you view fractals, you can magnify them an infinite number of times,
and they contain structure at every magnification level.   Second, you
can generate fractals using finite and typically small sets of
instructions and data.   Fractals grew out of the goal of
mathematicians to completely describe the world using standard
geometrical expressions.   IBM mathematician Benoit B. Mandelbrot, PhD,
proved and published the theory behind fractals in 1981 and was the
first to view computer-generated fractal structures.   The well-known
Mandelbrot Set is named in his honor.   Another famous fractal
researcher, with a set also named for him, is French mathematician
Gaston Julia.

The standard Mandelbrot fractal equation takes the form z(n+1) = z(n)^2 + c,
where c is the complex number x+iy corresponding to any point on the
(x,y) coordinate plane.   Fractal equations are iterative, in that the
result of one calculation of the fractal equation becomes the z input
to the next calculation.   Over repeated evaluations of a fractal
equation, values for each point in the (x,y) coordinate space either
converge at single points, move toward the (0,0) origin point, or move
toward infinity.   The diverse colors in fractal plots reflect the rate
of this movement for each point.   Discussions of chaos theory
frequently use fractals as examples, because slight variations in the
fractal equation produce radically different results.

~~~~~~~~~~~~~~~~~~~~~~~~~~~

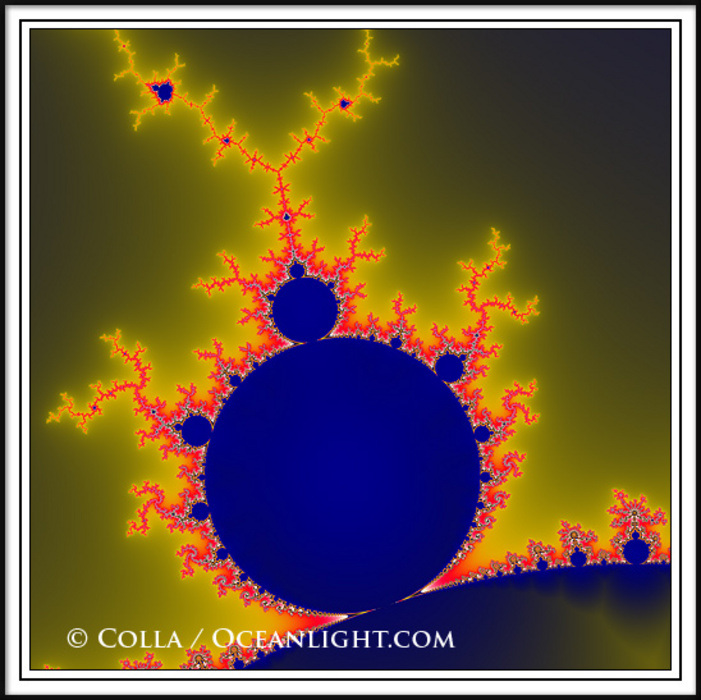
Detail within the Mandelbrot set fractal. This detail is found by
zooming in on the overall Mandelbrot set image, finding edges and buds
with interesting features. Fractals are complex geometric shapes that
exhibit repeating patterns typified by self-similarity, or the
tendency for the details of a shape to appear similar to the shape
itself. Often these shapes resemble patterns occurring naturally in the
physical world, such as spiraling leaves, seemingly random coastlines,
erosion and liquid waves. Fractals are generated through surprisingly
simple underlying mathematical expressions, producing subtle and
surprising patterns. The basic iterative expression for the Mandelbrot
set is z = z-squared + c, operating in the complex (real, imaginary)
number set.
Image: 10378  
Species: Mandelbrot set

at: www.oceanlight.com/log/mandelbrot-fractal-pic.